题目描述

$Mas$最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

$Mas$玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

• 在一个$n \times m$棋盘上有$n \times m$个格子，其中有且只有一个格子是空白的，其余$n \times m-1$个格子上每个格子上有一个棋子，每个棋子的大小都是$1 \times 1$的；

• 有些棋子是固定的，有些棋子则是可以移动的；

• 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩$q$次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第$i$次玩的时候，空白的格子在第$EX_i$行第$EY_i$列，指定的可移动棋子的初始位置为第$SX_i$行第$SY_i$列，目标位置为第$TX_i$行第$TY_i$列。

假设$Mas$每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。

请你告诉$Mas$每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入

每组输入数据的第一行有$3$个整数，每两个整数之间用一个空格隔开，依次表示$n、m$和$q$；

接下来的$n$行描述一个$n \times m$的棋盘，每行有$m$个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，$0$表示该格子上的棋子是固定的，$1$表示该格子上的棋子可以移动或者该格子是空白的。

接下来的$q$行，每行包含$6$个整数依次是$EX_i、EY_i、SX_i、SY_i、TX_i、TY_i$，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出

每组输出有$q$行，每行包含$1$个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出$−1$。

样例输入

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

样例输出

2
-1

数据规模：

对于$30\%$的数据，$1≤n, m≤10，q=1$；

对于$60\%$的数据，$1≤n, m≤30，q≤10$；

对于$100\%$的数据，$1≤n, m≤30，q≤500$。

样例解释：

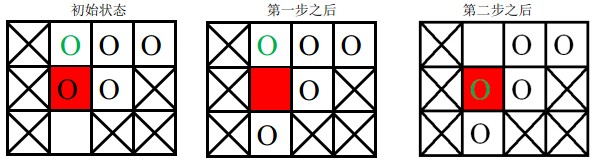
棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是$(3, 2)$（图中空白所示），游戏的目标是将初始位置在$(1, 2)$上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置$(2, 2$)（图中红色的格子）上。

移动过程如下：

第二次游戏，空白格子的初始位置是$(1, 2)$（图中空白所示），游戏的目标是将初始位置在$(2, 2)$上的棋子（图中绿色圆圈所示）移动到目标位置$(3, 2)$上。

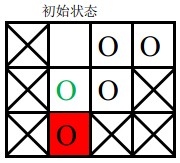
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置$(2, 2)$上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。