题目描述

“布朗运动”是指微小颗粒永不停息的无规则随机运动。在如图所示的实验容器中，容器由n个仓组成，某粒子作布朗运动时每次会从所在仓的通道口中随机选择一个到达相邻仓或容器外，一旦粒子到达容器外就会被外部捕获装置所捕获，此时试验结束。已知该粒子初始位置在1号仓，求试验结束时该粒子是从1号仓到达容器外的概率。

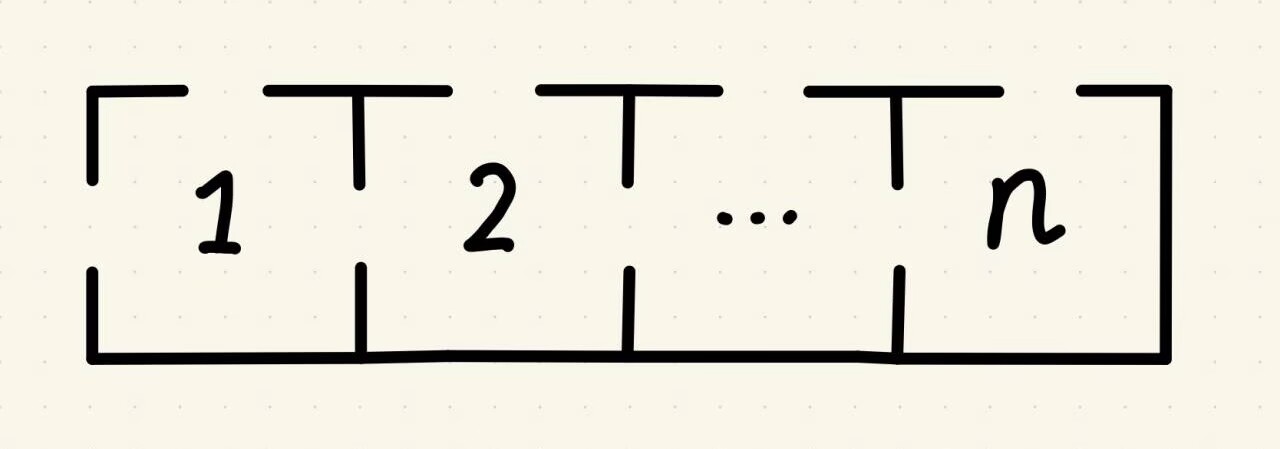
输入格式

输入一个整数n，表示此次试验有n个仓。

输出格式

输出一个最简分数，输出格式为分子/分母。

输入样例1

2

输出样例1

4/5

样例1解释

设$p_1$为粒子在1号仓内时最终从1号仓到达容器外的概率，$p_2$为粒子在2号仓时最终从1号仓到达容器外的概率。

则有关系式： $$p_1=\frac 2 3+\frac 1 3p_2$$ $$p_2=\frac 1 2p_1$$ 可解得 $p_1=\frac 4 5$

输入样例2

3

输出样例2

10/13

数据范围与约定

对于$10\%$的数据，$2\le n \le 3$. 对于$30\%$的数据，$2\le n \le 10$. 对于$100\%$的数据，$2\le n \le 40$.